有趣的圆形手抄报带字简单
一、圆的定义
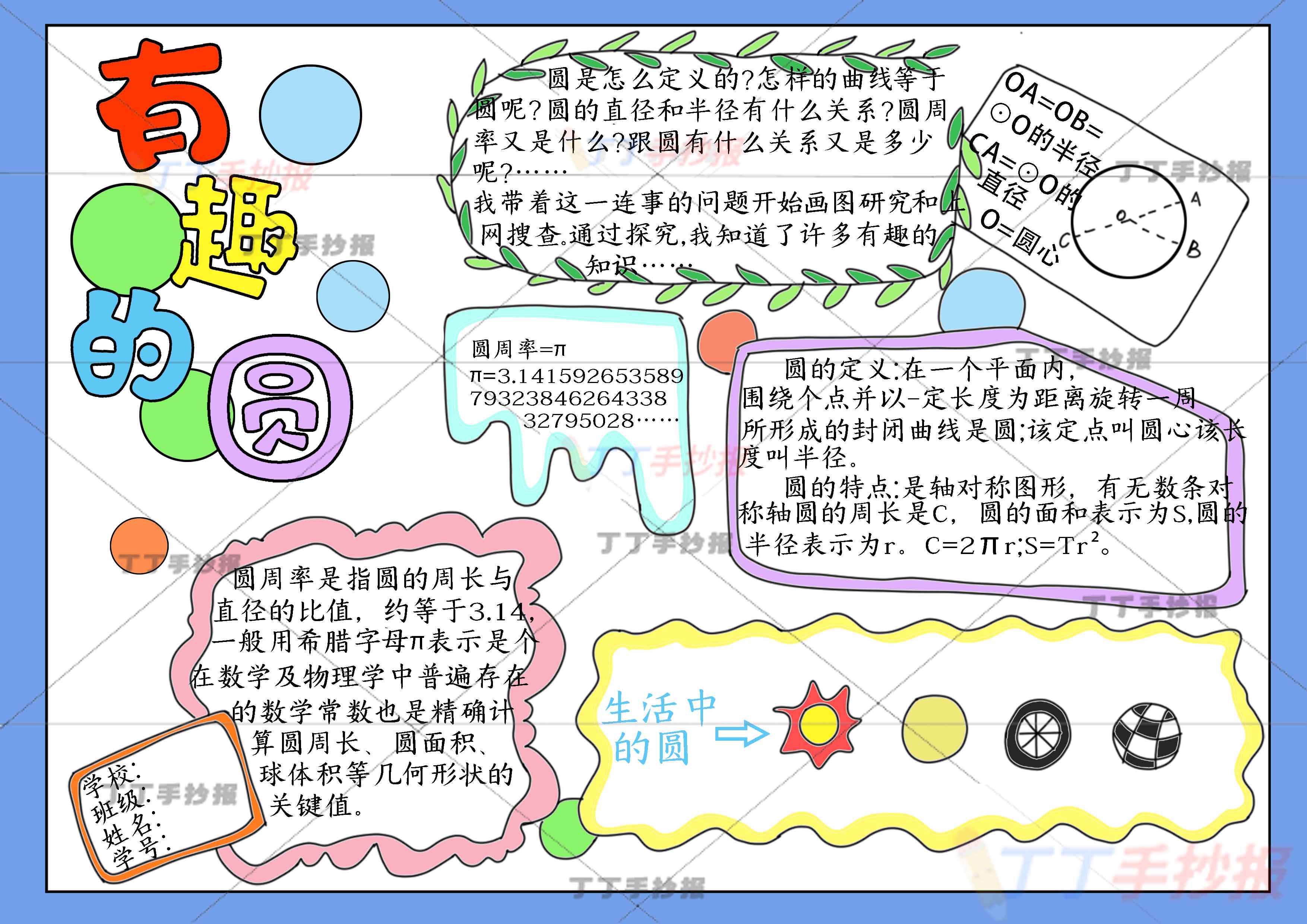
1、以定点为圆心,定长为半径的点组成的图形
2、在同一平面内,到一个定点的距离都相等的点组成的图形
二、圆的各元素
1、半径: 圆上一点与圆心的连线段
2、直径: 连接圆上两点有经过圆心的线段
3、弦: 连接圆上两点线段(直径也是弦)
4、弧: 圆上两点之间的曲线部分。半圆周也是弧。
(1)劣弧: 小于半圆周的弧
(2)优弧: 大于半圆周的弧
5、圆心角: 以圆心为顶点,半径为角的边。
6、圆周角: 顶点在圆周上,圆周角的两边是弦
7、弦心距: 圆心到弦的垂线段的长
三、圆的基本性质
1、圆的对称性
(1)圆是轴对称图形,它的对称轴是直径所在的直线。
(2)圆是中心对称图形,它的对称中心是圆心。
(3)圆是旋转对称图形
2、数学圆周率的由来
圆周率,一般以π来表示,是一个在数学及物理学普遍存在的数学常数。它定义为圆形之周长与直径之比值。它也等于圆形之面积与半径平方之比值。是精确计算圆周长、圆面积、球体积等几何形状的关键值。
在分析学上,π可以严格地定义为满足sin(x) = 0的最小正实数x。2011年6月部分学者认为圆周率定义不合理,要求改为6.28。
3、为什么要计算圆周率
其实,即使是要求最高、最准确的计算,也用不着这么多的小数位,那么,为什么人们还要不断地努力去计算圆周率呢?
第一,用这个方法就可以测试出电脑的毛病。如果在计算中得出的数值出了错,这就表示硬件有毛病或软件出了错,这样便需要进行更改。同时,以电脑计算圆周率也能使人们产生良性的竞争,科技也能得到进步,从而改善人类的生活。就连微积分、高等三角恒等式,也是由研究圆周率的推动,从而发展出来的。
第二,数学家把π算的那么长,是想研究π的小数是否有规律。比如,π值从第70.01万位小数起,连续出现7个3,即3333333,从第320.4765万位开始,又连续出现7个3。
-
上一篇:数学日记手抄报女孩
- 下一篇:数学英语手抄报男孩女孩积木
热门手抄报
-

克千克吨的认识手抄报带字苹果小女孩
2025-03-20 825 -

二年级下册数学手抄报吃西瓜男孩思维导图
2025-10-03 412 -

数学克与千克手抄报女孩可爱
2025-03-20 342 -

二年级下册数学混合运算手抄报四边框
2025-04-15 245 -

旅行中的数学手抄报带字椰子
2025-03-20 222 -

二年级数独手抄报向日葵边框
2025-03-20 222 -
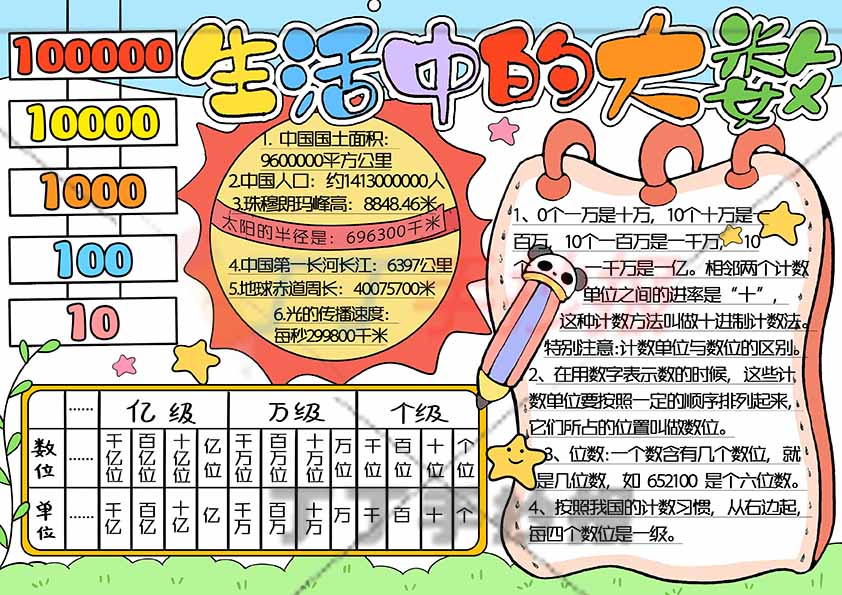
生活中的大数手抄报四年级数学数位表
2025-03-20 218 -

二年级数独手抄报铅笔边框
2025-03-20 215 -
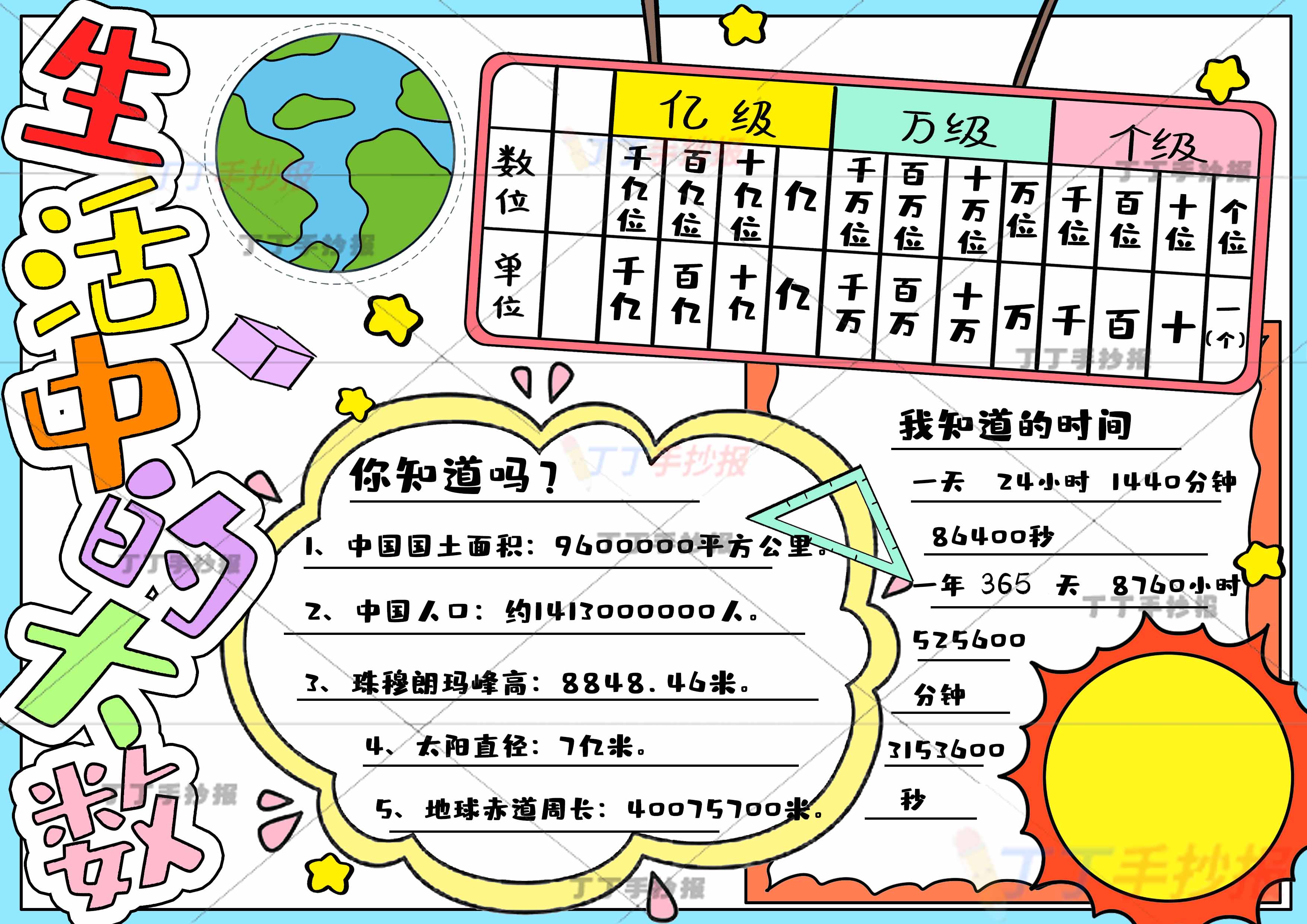
生活中的大数手抄报四年级数学右下角太阳
2025-03-20 208 -
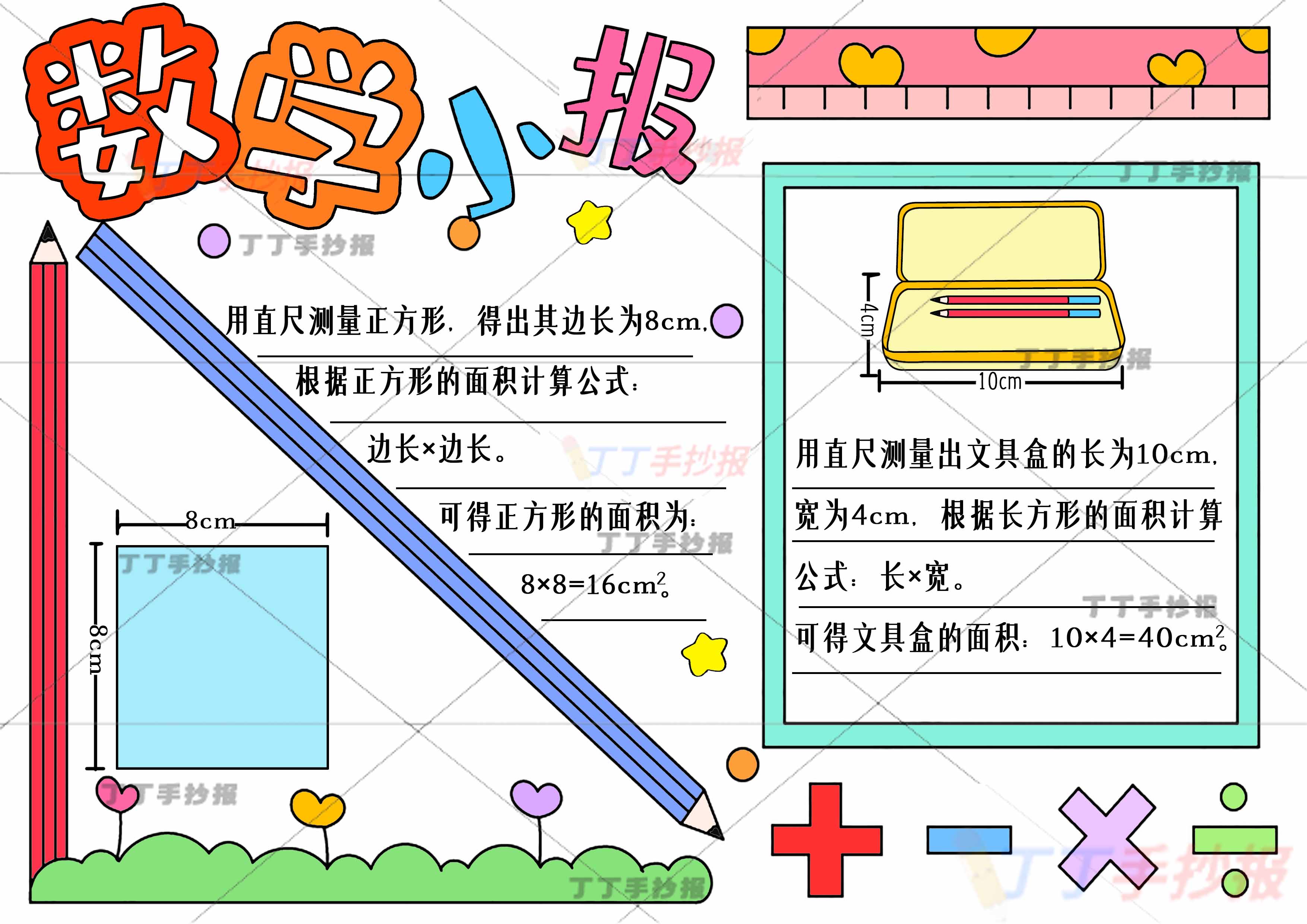
数学小报手抄报测量文具盒
2025-03-20 198